Je viens de faire un tutoriel vidéo pour montrer le potentiel d’un outil de conception optique open source sur lequel je suis tombé dernièrement : FreeCAD Optics Workbench. En quelques minutes, on peut convertir un simple CAD 3D du fabricant en lentille, faire un tracé de rayons et obtenir un scatter plot. Ça se limite à l’optique géométrique, mais c’est bien suffisant dans bon nombre de situations.
Optique
Calcul de la résolution spectrale d’un spectromètre
Dispersion spectrale du système
Une fente de hauteur h est placée au plan focal d’une lentille convexe ou d’un miroir concave. En utilisant l’approximation paraxiale, l’angle produit par cette hateur est donnée par theta ~= h/f, où h est la hauteur de la fente et f la longueur focale. On peut le voir selon l’optique de Fourier : la fente de largeur h produit un angle de largeur theta à la sortie de la lentille. On place le réseau à cet endroit, et il crée lui aussi une dispersion angulaire, selon l’équation sin(theta)=m*d*lambda, où m est l’orde de diffraction, d le pas du réseau (lignes/mm) et lambda la longueur d’onde. Pour un angle plus petit que h/f, on ne saura pas si la dispersion provient du réseau (donc de la longueur d’onde) ou bien de l’optique d’entrée (indépendante de la longueur d’onde). Puisque nous souhaitons différencier les longueurs d’onde pour obtenir un spectre, cela nous donne l’équation de la limite de résolution du système (en posant dans les deux cas sin(theta)=theta ) : h/f = m*d*delta_lambda => delta_lambda = h/(m*d*f).
À titre d’exemple, pour une fente de 63 um, une focale de 100 mm, un pas de 600 lignes/mm et l’ordre 1, on obtient une résolution de 1nm.

Largeur spectrale
Il y a un repliement spectral inhérent à l’équation du réseau. J’avais oublié ceci, c’est expliqué dans le Hecht à la page 481. En bref, il n’est pas possible de faire la distinction entre l’ordre m+1 et la longueur d’onde lambda/(m+1). Par exemple, un réseau produira la même dispersion angulaire pour une longueur d’onde de 600nm à l’ordre 1, que 300nm à l’ordre 2. Cela limite donc la largeur spectrale à lambda_max /2. Des techniques supplémentaires doivent être utilisées pour tenir compte de cet effet. Pour l’instant, il suffit de le garder en tête et je verrai quoi faire selon l’application.
Optique et fente de sortie
On doit s’assurer que h2f2 <= h1f1, autrement dit, que la fente de sortie et la focale de la lentille de sortie soient égales ou plus petites que les paramètres d’entrée. Le plus simple est souvent de garder les mêmes valeurs, soit ici 63 um et 100 mm. Si pour une raison ou une autre, cela n’est pas le cas, ce sera ce paramètre qui limitera la résolution finale du système. Par exemple, si je mets une photodiode de 1mm sans fente à la sortie du spectromètre, même si la fente d’entrée est de 63 um, la résolution spectrale sera de 17nm.
Aberrations du système optique
Jusqu’à maintenant, on utilisait des optiques sans défaut (et l’équation paraxiale!). Dans la vraie vie, les aberrations peuvent souvent limiter la résolution specrtale d’un système. La meilleure approche est toujours de diminuer l’ouverture numérique : augmenter la focale et diminuer les hauteurs des composants. Pour réduire les coûts, j’ai choisi un design à un seul miroir concave avec une focale de 100mm, et le plus petit réseau, soit 12,7mm de large. On verra plus loin que l’on a encore une marge de manoeuvre pour la limite posée par la diffraction de ces ouvertures. J’utilise OSLO pour simuler le tout. Je suis parti de la lentille d’exemple du monochromateur et je l’ai modifié comme suit :
// OSLO 22.2.0.22257 20041 0 34476
LEN NEW "Spectrometre 300-1700nm" -1e+20 4
NAO 0.08
OBH 1.0e-06
DES "Fred"
UNI 1.0
SNO1 "This is a very simple but interesting spectrograph. It is telecentric and"
SNO2 "afocal, but is used as a focal system. The grating is square, so the ebr must"
SNO3 "be oversized by sqrt(2) to fill it. The default drawing rays have been set at"
SNO4 "fy=0.6 so they pass within the checked grating aperture. Try interactive design"
SNO5 "and vary the object decenter and the grating tilt to see how this system works."
SNO10 "DIFFRACTIVE"
// SRF 0
AIR
TH 100.0
AP 1.0e-06
DT 1
DCY -15.0
NXT // SRF 1
RFH
RD -200.0
TH -100.0
AP 25.0
NXT // SRF 2
RFH
TH 100.0
AP 6.4
AST
DT 1
TLA -31.0
APN 1
AY1 0 -6.3
AY2 0 6.3
AX1 0 -6.3
AX2 0 6.3
ATP 0 2
AAC 0 4
GOR 1
GSP 0.0016667
RCO 0
NXT // SRF 3
RFL
TCE 236.0
PK CV -2 0.0
TH -100.0
PK AP -2
NXT // SRF 4
AIR
AP 25.0
CBK 1
RAIM Tel
WV 1.7
WW 1.0
END 4
DLID 100.0
DLFD 100.0
DLMN 0 -0.65
DLMX 0 0.65
DLNR 1 3
DLFP 1 0.0
DLMN 1 -0.65
DLMX 1 0.65
DLWN 1 2
DLFP 2 0.0
DLMN 2 -0.65
DLMX 2 0.65
DLWN 2 3L’ouverture numérique du système est de 0,08. Dans la construction, il faudra rajouter des stops quelque part pour la respecter, sinon la lumière pourrait se rendre jusqu’au détecteur par d’autres chemins. L’utilisation d’une fibre optique à NA=0,1 pourrait aussi être une bonne solution. Le schéma ressemble à ceci :

J’ai mis la longueur d’onde maximale, soit 1700nm, pour que le réseau ait l’angle maximal et produise ainsi le plus d’aberration. Je m’attends à ce qu’il y ait de l’aberration sphérique, de la coma et de l’astigmatisme, et sûrement autre chose. L’utilisation d’un miroir élimine les aberrations chromatiques, qui seraient ingérables sur une aussi grande bande spectrale. Dans mon cas, ce qui m’intéresse, c’est la largeur de la tache (spot size) produit par la somme de toutes les aberrations. Selon la simulation, cela donne ceci :
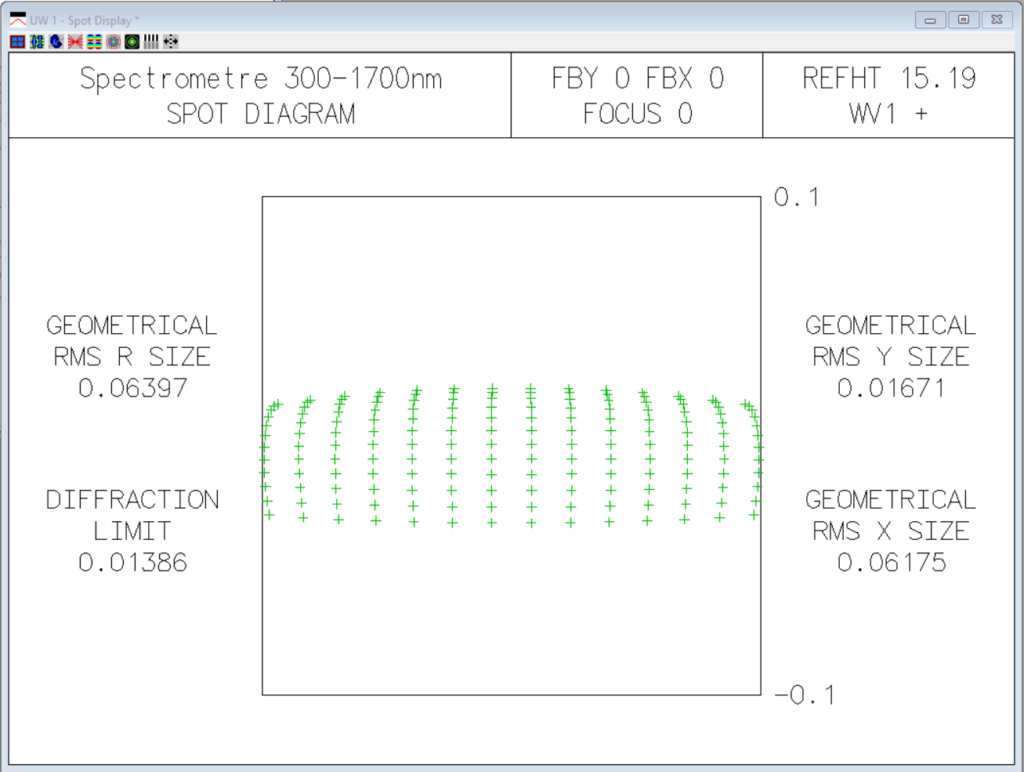
Le spectre sera selon l’axe y, donc la valeur à retenir est 0,017mm. On pourrait donc théoriquement avoir une fente aussi petite que cela, pour une résolution du sytème à ~0,27nm. Par contre, on perdrait le signal qui s’étalerait tout de même sur 62um en x. Notons que le résutat est très proche de la limite de la diffraction, soit 0,014mm. Cela veut dire que si l’on voulait aller chercher une meilleure résolution que 0,27nm, il faudrait grossir les composantes. J’utilie déjà le miroir standard le plus large (50mm), il faudrait donc utiliser deux miroirs, ou bien un miroir plus large et donc beaucoup plus dispendieux. Pour conserver une ouverture numérrique basse, le système devra également avoir des focales plus grandes, etc. Je souhaite produire un instrument portable et peu dispendieux, ces contraintes sont à prendre en considération.
Diffraction du réseau
Il est important que le réseau soit le plus possible en condition de pleine illumination, car la diffraction produite par N fentes pose également une limite à la résolution. L’équation est donnée dans le Hecht à la page 481 :
lambda / delta_lamba = mN, où N = dL est le nombre de lignes total du réseau, d est le pas du réseau et L la largeur
En réarrangeant l’équation, on a :
delta_lambda = lambda / (m * d * L)
Prenons le cas extrême dans mon exemple, 1700nm : on a une diffraction de 1700nm / (1 * 600mm^-1*12,7mm) = 0,22nm. Pour descendre en résolution, il faudrait un réseau plus large ou avec un pas plus dense. Comme je m’en suis rendu compte dans mon article prédédent, 600 lignes/mm est le maximum pour obtenir des angles raisonnables à 1700nm. La seule solution est encore une fois d’avoir un réseau plus large, donc un système optique plus large. Je vais me satisfaire du design actuel, puisque ce n’est pas cet effet qui limite la résolution.
Précision mécanique de l’angle du réseau
C’est bien beau les simulations, mais dans les faits, il va falloir aligner tout ça comme il faut. On verra comment je réussirai à assembler tout ça. Pour les fins de la simulation, le paramètre important est la résolution angulaire du moteur. Dans ce type de spectromètre, la fente d’entrée et de sortie gardent leur position, et on scanne les longueurs d’onde en faisant tourner le réseau. Par exemple, selon la simulation OSLO, pour une longueur d’onde de 300nm, il faudra mettre le réseau à un angle de -5,5deg, et pour 1700nm, ce sera -31deg. En approximant le tout comme étant linéaire, on obtient environ 0,018deg/nm. L’encodeur que je souhaite utiliser est spécifié à 0,011deg de résolution. Je pourrai donc garantir une résolution de 1nm. Je pourrais aller plus bas en microstepping, mais je n’aurais pas la certitude que mécaniquement l’angle soit réellement changé. Je pourrais aussi utiliser une boîte d’engrenages, mais cela vient avec des problèmes supplémentaires : backlash et répétabilité.
Conclusion
On voit que pour plein de raisons, la limite de la résolution spectrale tourne autour de 1nm dans mon design. Aller au-delà demande une complexité dans laquelle je ne suis pas prês de m’aventurer. Ce sera déjà un bon défi d’atteindre ce niveau de performance avec les pièces que j’ai choisies.
Plage d’utilisation d’un réseau de diffraction
Je suis en train de concevoir un spectromètre de type Czerny–Turner. En le simulant sur OSLO, je me suis rendu compte d’une propriété que j’avais oubliée : pour chaque valeur de pas (lignes par mm), il y a une longueur d’onde maximale au-delà de laquelle l’angle de diffraction de l’ordre 1 dépasse physiquement les dimensions du spectromètre.
Dans mon cas, j’utilise un réseau en réflexion et un miroir concave. L’équation de la diffraction est :
sin(theta_m) – sin(theta_i) = m*d*lambda
où theta_m est l’angle diffracté, theta_i l’angle d’incidence, m l’ordre de diffraction, d le pas du réseau et lambda la longueur d’onde de la lumière.
En postulant theta_m = 2*theta_i (le faisceau réfracté revient sur le parcours du faisceau incident après une réflexion sur le réseau tourné à un angle -theta_i), approximation qui vient du fait que l’on souhaite avoir une longue focale pour les optiques pour avoir une bonne résolution, on trouve :
sin(2*theta_i) – sint(theta_i) = m*d*lambda
Si l’on trouve le maximum de la partie gauche de l’équation (https://www.wolframalpha.com/input?i=max%28sin%282x%29-sin%28x%29%29), on obtient 1,76.
J’étais vraiment curieux de la manière dont on obtient cette solution, alors j’ai payé la version pro de wolfram juste pour le savoir. On commence évidemment par faire la dérivée de l’expression et la mettre égale à zéro, ce qui fait 2cos(2x)-cos(x)=0. Rendu là, j’étais bloqué, parce que je ne trouvais aucune identité trigonométrique pour m’avancer en quoi que ce soit. Bien sûr, un calcul numérique serait possible, mais j’étais sûr qu’une solution analytique existe. L’identité magique à utiliser est en fait cos(2x) = 2cos^2(x) – 1. En l’utilisant, on obtient une fonction quadratique de cos(x) : -2-cos(x)+4cos^2(x)=0, qui se résout de la manière usuelle, en faisant attention aux signes et aux cadrant des angles. Bref, toutes ces mathématiques commençaient à être loin, un petit rappel a fait du bien.
Pour un réseau de 1200 lignes/mm (que je prévoyais utiliser initialement), la longueur d’onde maximale pouvant être diffractée vers l’optique est de :
1,76 / (1*1200mm⁻1) = 1,47um.
Étant donné que j’ai l’intention de mesurer des sources à 1550nm avec ce spectromètre, je dois modérer mes ardeurs et descendre à 600 lignes/mm. Ce qui fait prendre un coup à ma résolution spectrale, mais au moins, les angles sur le réseau sont plus réalistes. À 600 lignes/mm, la longueur d’onde maximale est le double, soit 2,94um. Pour l’instant, je prévois utiliser une photodiode InGaAs, qui peut détecter la lumière juqu’à 1700nm, ce qui posera la limite supérieure de mon spectromètre.
Comment brancher une photodiode 101
Je mets ça ici parce que je l’oublie périodiquement et que c’est la base de tous mes projets impliquant un mélange d’optique-photonique et d’électronique.
p. 842 du Art of Electronics 3rd edition

Figure A : la photodiode est en mode photovoltaîque (photocourant, en tout cas). Le voltage à sa jonction est de 0V. Le courant est transformé en voltage avec un gain V=RI par l’ampli transimpédance. Cette configuration minimise le dark current, mais est un peu plus lente (la capacitance de la jonction fait un filtre passe-bas avec la résistance). Meilleur SNR, moins de vitesse de réponse. Mode privilégié pour la plupart des projets.
Figure B : la photodiode est biaisée avec un voltage Vb, ce qui diminue sa capacitance, mais ajoute aussi le courant de fuite au dark noise. Le circuit est plus rapide, mais a un SNR plus faible.
Vidéo sur mon télescope à réalité augmentée
J’ai réalisé une vidéo sur mon projet de télescope à réalité augmentée. Je l’ai présenté en long et en large dans les articles précédents. L’ajout dont je n’ai pas parlé est l’arduino et le BMP085 (un capteur de température et de pression), permettant d’afficher sur l’écran LCD les données de température et d’altitude en temps réel. L’arduino envoie une commande par un port série à la carte Nextion, qui actualise les données affichées à l’écran. Le code arduino, basé sur les exemples de Nextion (je n’arrive plus à retrouver le lien) est le suivant :
#include <SoftwareSerial.h>
#include <Wire.h>
#include <Adafruit_Sensor.h>
#include <Adafruit_BMP085.h>
SoftwareSerial mySerial(10, 11); /*Even though you can use the hardware serial port in this case I think it is better to
leave the hardware serial open for debugging purposes*/
Adafruit_BMP085 bmp = Adafruit_BMP085(10085);
float temperature;
void setup() {
Serial.begin(57600); //open the hardware serial port
while (!Serial) { // wait for serial port to connect. Needed for native USB port only
;
}
/* Initialise the sensor */
if(!bmp.begin())
{
/* There was a problem detecting the BMP085 … check your connections */
Serial.print(« Ooops, no BMP085 detected … Check your wiring or I2C ADDR! »);
while(1);
}
Serial.println(« Serial On »); //Print this messages when the serial port is connected
mySerial.begin(9600); // set the data rate for the SoftwareSerial port
}
void loop() {
/* Get a new sensor event */
sensors_event_t event;
bmp.getEvent(&event);
/* Display the results (barometric pressure is measure in hPa) */
if (event.pressure)
{
/* Display atmospheric pressue in hPa */
Serial.print(« Pressure: « );
Serial.print(event.pressure);
Serial.println( » hPa »);
/* Calculating altitude with reasonable accuracy requires pressure *
* sea level pressure for your position at the moment the data is *
* converted, as well as the ambient temperature in degress *
* celcius. If you don’t have these values, a ‘generic’ value of *
* 1013.25 hPa can be used (defined as SENSORS_PRESSURE_SEALEVELHPA *
* in sensors.h), but this isn’t ideal and will give variable *
* results from one day to the next. *
* *
* You can usually find the current SLP value by looking at weather *
* websites or from environmental information centers near any major *
* airport. *
* *
* For example, for Paris, France you can check the current mean *
* pressure and sea level at: http://bit.ly/16Au8ol */
/* First we get the current temperature from the BMP085 */
float temperature;
bmp.getTemperature(&temperature);
Serial.print(« Temperature: « );
Serial.print(temperature);
Serial.println( » C »);
/* Then convert the atmospheric pressure, SLP and temp to altitude */
/* Update this next line with the current SLP for better results */
float seaLevelPressure = SENSORS_PRESSURE_SEALEVELHPA;
Serial.print(« Altitude: « );
float alt = bmp.pressureToAltitude(seaLevelPressure,
event.pressure,
temperature);
Serial.print(alt);
Serial.println( » m »);
Serial.println(« »);
String sendThis = « »; //Declare and initialise the string we will send
delay(300); //Probably unneccessary, but I give the screen some time to respond
sendThis = « n0.val= »; //Build the part of the string that we know
sendThis.concat(int(temperature)); //Add the variable we want to send
writeString(sendThis); /*Use a function to write the message character by character to the Nextion because
mySerial.write(sendThis) gives you an error due to a datatype mismatch*/
delay(300); //Probably unneccessary, but I give the screen some time to respond
sendThis = « n1.val= »; //Build the part of the string that we know
sendThis.concat(int(alt)); //Add the variable we want to send
writeString(sendThis); /*Use a function to write the message character by character to the Nextion because
mySerial.write(sendThis) gives you an error due to a datatype mismatch*/
}
else
{
Serial.println(« Sensor error »);
}
}
//NOTE: A great big thanks to: RamjetX for writing this function. You can find his/her post here: http://forum.arduino.cc/index.php?topic=89143.0. Please go give him/her some Karma!
void writeString(String stringData) { // Used to serially push out a String with Serial.write()
for (int i = 0; i < stringData.length(); i++)
{
mySerial.write(stringData[i]); // Push each char 1 by 1 on each loop pass
}
mySerial.write(0xff); //We need to write the 3 ending bits to the Nextion as well
mySerial.write(0xff); //it will tell the Nextion that this is the end of what we want to send.
mySerial.write(0xff);
}// end writeString function
Défrichage de fibre optique pour l’imagerie oxymétrique
Parce que oui, c’est possible de faire autre chose que des sapins de Noël avec de la fibre en PMMA à 10¢ le mètre. Je me suis lancé sérieusement, dans les derniers jours, dans mon projet d’imagerie oxymétrique. Pour commencer, j’ai découpé 147 bouts de 30 centimètres afin d’avoir une image composée d’un carré de 7×7 (ou toute autre forme comprenant 49 bouts de fibre sur l’image de la caméra).
Sources lumineuses
En utilisant deux sources de longueur d’onde différente, l’une dans le rouge, l’autre dans l’infrarouge, il est possible de déterminer le taux d’hémoglobine oxygénée par rapport à l’hémoglobine désoxygénée, en se basant sur les courbes d’absorption particulières. Ce principe est largement utilisé dans les sphygmo-oxymètres optiques, mesurant la concentration d’oxygène en un point (normalement un doigt) et supposant qu’elle est homogène dans le reste du corps. Or, la consommation d’oxygène par les organes varie selon l’effort énergétique qu’ils doivent fournir. En ayant une méthode qui permet de mesurer les variations d’oxygénation dans un volume donné, on ouvre la porte à toutes sortes d’applications intéressantes, comme l’imagerie spectroscopique proche infrarouge fonctionnelle (functional near-infrared imaging, fNIR, en anglais), ce qui est très excitant puisqu’elle permet de visualiser les processus mentaux en temps réel avec, ce que je souhaite vérifier, du matériel très peu coûteux et facile à trouver.
 (source : http://www.oximetry.org/pulseox/principles.htm)
(source : http://www.oximetry.org/pulseox/principles.htm)
Atténuation de la fibre
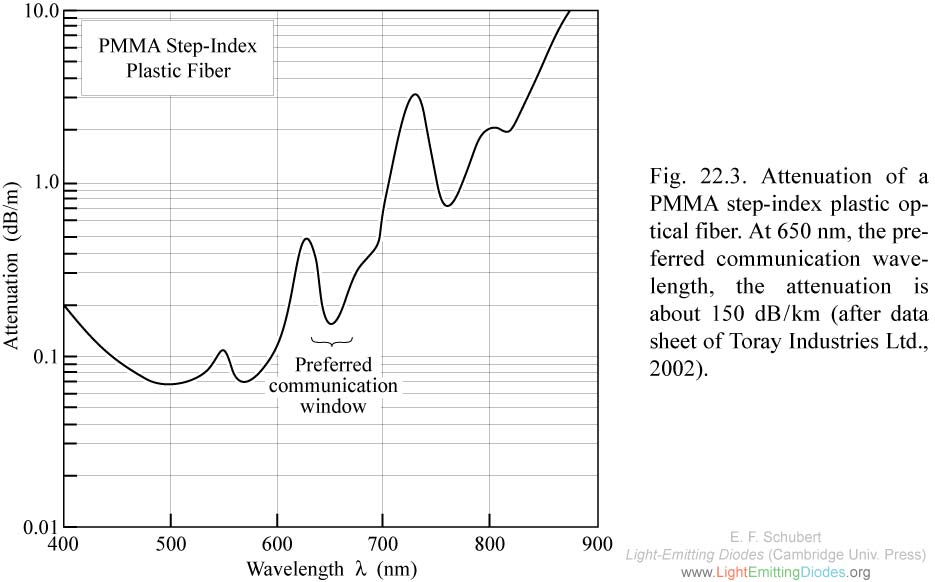
L’atténuation dans le proche-infrarouge pour le PMMA grimpe rapidement, comme on peut le voir sur le graphique. À 850nm, on a environ 5dB/m d’atténuation. Il faut donc garder les bouts de fibre très courts. Avec 30 centimètres, les pertes sont de 1,5dB (~71% du signal est transmis), ce qui fait mal, mais pas trop, espérons-le.
Matériel
Pour mes sources lumineuses, j’utilise deux DEL à très haute puissance optique (2,6W) afin d’être certain d’avoir suffisamment de signal. J’aurais pu utiliser des lasers, mais mon objectif était d’injecter simultanément toutes les fibres, le plus simplement possible. De plus, les DEL sont moins coûteuses et moins dangereuses (quoique à cette puissance, même si ce n’est pas un faisceau cohérent, j’ai tendance à être prudent quand même).
Je les avais déjà préalablement soudées l’année passée, lorsque j’avais commencé ce projet. Je leur ai rajouté un petit cylindre imprimé en 3D, qui se met directement autour du petit bulbe-lentille de la DEL et qui est suffisamment large pour y faire tenir les 49 fibres.

J’utilise pour les alimenter un power supply d’ordi, qui me donne 15V et 5A, le tout régulé à 700mA par diode par des régulateurs spécialisés pour cette application.

J’ai remarqué qu’allumées à pleine puissance, elles deviennent très chaudes très rapidement, ce qui va être à tenir en compte dans la suite du projet. Il va falloir soit les utiliser périodiquement avec un rapport cyclique faible, soit rajouter un système de refroidissement adéquat, ou bien y aller avec une combinaison de ces deux approches.

À 850nm, l’oeil perçoit un rouge très faible, sûrement la limite inférieure du spectre de la diode, qui est en fait bien plus lumineuse, tel qu’on peut l’observer avec la caméra qui lui donne une couleur mauve.


La DEL à 660nm est extrêmement brillante, puisque la quasi-totalité de son spectre est dans le visible. On peut voir que les fibres contiennent bien le faisceau.
Pour la caméra, j’utilise une caméra de drone de marque RunCam qui a une sensibilité absolument phénoménale pour son prix abordable : jusqu’à 0,0001 Lux (elle m’avait coûté 50$US si je me souviens bien). Je lui ai imprimé en 3D un petit adaptateur qui rassemble toutes les fibres et y fait tenir la caméra. Toutefois, comme on peut le voir sur la dernière image, ce sera à refaire puisque le focus de la caméra est à l’infini, ce qui mélange toutes les fibres en un gros blob de lumière. Il va donc falloir rajouter de l’optique pour imager correctement les fibres et arriver à les distinguer individuellement afin de pouvoir traiter le signal. C’est le pari à relever en ce moment dans ce projet.



