Auteur : Frederik

Conception

J’ai décidé de redonner un tour de roue à mon projet philati (https://hackaday.io/project/9641-lati), plus précisément au capteur de respiration le composant. J’ai principalement fait un PCB qui contient le pont de Wheatstone, l’ampli d’instrumentation et les filtres analogiques. Un Adafruit Feather nrf52840 Express est utilisé comme microcontrôleur.

La ceinture est faite à partir d’une bande élastique et de « buckles » (attache? j’ai aucune idée du mot en français) que j’ai achetés sur un site de matériel de plein air. La pièce qui tient le PCB et les moteurs haptiques est imprimée en TPU. Voici le code OpenSCAD :

$fn=100;
re = 150; //rayon extérieur
ep = 4; 

difference(){
    cylinder(d=re,h=ep);
    cylinder(d=re-50,h=ep);
    
    //Trous pour la sangle
    translate([re/2-10,-26/2,0]) cube([4,26,ep]);
    translate([re/2-10-8,-26/2,0]) cube([4,26,ep]);
    translate([-re/2+10-4,-26/2,0]) cube([4,26,ep]);
    translate([-re/2+10-4+8,-26/2,0]) cube([4,26,ep]);
    
    //Trous pour les moteurs
    for (theta = [22.5 : 45 : 337.5]){
        rotate([0,0,theta]) translate([(re-25)/2,0,0.3]) cylinder(d=16,h=ep);
    }
}

difference(){
    union(){
        translate([-5,-70]) cube([10,140,ep]);
        translate([-(43+ep)/2, -(56+ep)/2]) cube([43+ep,56+ep,7]);
    }
    translate([-43/2, -56/2,1]) cube([43,56,7]);
}

Le capteur de respiration est toujours le fil en caoutchouc conducteur trouvé sur Adafruit (https://www.adafruit.com/product/519). Il est simplement serré autour de deux broches branchées sur chaque bout du fil. Je ne m’attarderai pas sur la conception du circuit, parce que je l’ai déjà documenté dans mon projet philati. Je mets tout de même ici le schéma et le dessin du PCB, comme référence.

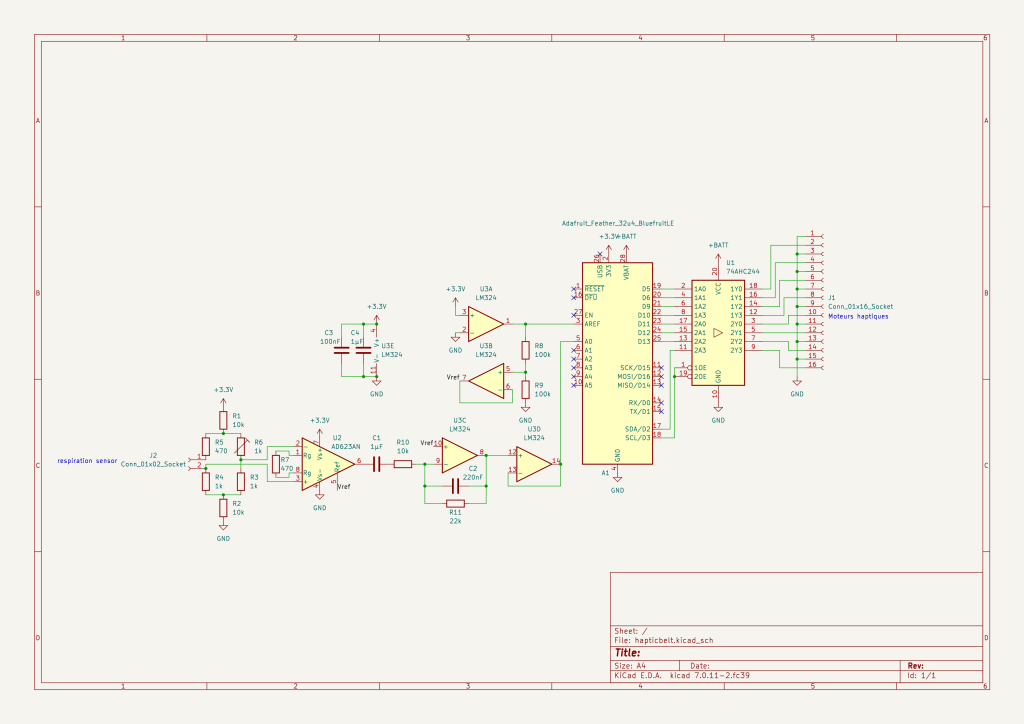
J’ai réussi à à peu près tout rentrer en-dessous du board du feather, pour un design compact et en utilisant uniquement des composantes trough hole.

L’autre partie du projet inclut une évolution de ma ceinture haptique, qui contient 8 moteurs haptiques de vibration en rotation, placées dans l’anneau de TPU, collés sur une mince couche de 0,3 mm d’épais. L’élasticité du matériau permet au moteur de bouger assez librement, tout en étant fixé à la colle chaude. La surface lisse en-dessous de l’anneau peut ainsi être placée directement sur la peau si on veut. J’utilise le PWM sur les pins et un simple buffer logique pour alimenter les moteurs. La spécification en courant ne permet pas d’alimenter tous les moteurs en même temps, mais le maximum que j’ai besoin pour les effets est de seulement deux moteurs à la fois.

Je n’ai pas encore mélangé les deux programmes du microcontrôleur, j’ai mis une pause sur le projet après des tests préliminaires pour les raisons que j’explique plus loin. Le code arduino pour transmettre les données du capteur de respiration à un ordi ressemble à ceci :

/*********************************************************************
 This is an example for our nRF52 based Bluefruit LE modules

 Pick one up today in the adafruit shop!

 Adafruit invests time and resources providing this open source code,
 please support Adafruit and open-source hardware by purchasing
 products from Adafruit!

 MIT license, check LICENSE for more information
 All text above, and the splash screen below must be included in
 any redistribution
*********************************************************************/
#include <bluefruit.h>
#include <Adafruit_LittleFS.h>
#include <InternalFileSystem.h>
#include "elapsedMillis.h"

// BLE Service
BLEDfu  bledfu;  // OTA DFU service
BLEDis  bledis;  // device information
BLEUart bleuart; // uart over ble
BLEBas  blebas;  // battery

const byte numChars = 16;
char receivedChars[numChars]; // an array to store the received data
boolean newData = false;
int peltierpin = 6;

#define SAMPLE_LEN 32 //Tel que configuré actuellement, bleuart peut seulement envoyer 64 bytes à chaque 1s
char sendBuffer[2*SAMPLE_LEN]; //Le buffer à envoyer par bluetooth
uint16_t* samplept = (uint16_t*)sendBuffer; //Lit le buffer en le considérant comme du 16 bits
uint8_t samplecnt = 0;
elapsedMicros bufferTimer; // Timer qui surveille le temps entre les enregistrements

void setup()
{
  pinMode(peltierpin, OUTPUT);
  digitalWrite(peltierpin, LOW);
  analogWriteResolution(15); //Met la fréquence du PWM à 514kHz, avec 5 bits de résolution (0-31)
  //analogWrite(peltierpin, 16384);
  analogReadResolution(14); //Les ADC lisent en 14 bits
  Serial.begin(115200);

#if CFG_DEBUG
  // Blocking wait for connection when debug mode is enabled via IDE
  while ( !Serial ) yield();
#endif
  
  Serial.println("Bluefruit52 BLEUART Example");
  Serial.println("---------------------------\n");

  // Setup the BLE LED to be enabled on CONNECT
  // Note: This is actually the default behavior, but provided
  // here in case you want to control this LED manually via PIN 19
  Bluefruit.autoConnLed(true);

  // Config the peripheral connection with maximum bandwidth 
  // more SRAM required by SoftDevice
  // Note: All config***() function must be called before begin()
  Bluefruit.configPrphBandwidth(BANDWIDTH_MAX);
  
  Bluefruit.begin();
  Bluefruit.setTxPower(4);    // Check bluefruit.h for supported values
  //Bluefruit.setName(getMcuUniqueID()); // useful testing with multiple central connections
  Bluefruit.Periph.setConnectCallback(connect_callback);
  Bluefruit.Periph.setDisconnectCallback(disconnect_callback);

  // To be consistent OTA DFU should be added first if it exists
  bledfu.begin();

  // Configure and Start Device Information Service
  bledis.setManufacturer("Adafruit Industries");
  bledis.setModel("Bluefruit Feather52");
  bledis.begin();

  // Configure and Start BLE Uart Service
  bleuart.begin();

  // Start BLE Battery Service
  blebas.begin();
  blebas.write(100);

  // Set up and start advertising
  startAdv();

  Serial.println("Please use Adafruit's Bluefruit LE app to connect in UART mode");
  Serial.println("Once connected, enter character(s) that you wish to send");
}

void startAdv(void)
{
  // Advertising packet
  Bluefruit.Advertising.addFlags(BLE_GAP_ADV_FLAGS_LE_ONLY_GENERAL_DISC_MODE);
  Bluefruit.Advertising.addTxPower();

  // Include bleuart 128-bit uuid
  Bluefruit.Advertising.addService(bleuart);

  // Secondary Scan Response packet (optional)
  // Since there is no room for 'Name' in Advertising packet
  Bluefruit.ScanResponse.addName();
  
  /* Start Advertising
   * - Enable auto advertising if disconnected
   * - Interval:  fast mode = 20 ms, slow mode = 152.5 ms
   * - Timeout for fast mode is 30 seconds
   * - Start(timeout) with timeout = 0 will advertise forever (until connected)
   * 
   * For recommended advertising interval
   * https://developer.apple.com/library/content/qa/qa1931/_index.html   
   */
  Bluefruit.Advertising.restartOnDisconnect(true);
  Bluefruit.Advertising.setInterval(32, 244);    // in unit of 0.625 ms
  Bluefruit.Advertising.setFastTimeout(30);      // number of seconds in fast mode
  Bluefruit.Advertising.start(0);                // 0 = Don't stop advertising after n seconds  
}

void loop()
{

  if (bufferTimer >= 100) { //parce que le code BLE est asynchrone, on doit utiliser un timer au lieu du delay
    //À 50ms, on sample à 20Hz
    samplept[samplecnt] = analogRead(A0);
    samplecnt = samplecnt + 1;
    bufferTimer = 0;
  }
  if (samplecnt == SAMPLE_LEN) {
    bleuart.write( sendBuffer, SAMPLE_LEN * 2 );
    samplecnt = 0;
  }
  //pollbleuart();
  //updatePeltier();
}

void pollbleuart() {
  static byte ndx = 0;
  char endMarker = '\n';
  char rc;
  
  while (bleuart.available() > 0 && newData == false) {
    rc = bleuart.read();

    if (rc != endMarker) {
      receivedChars[ndx] = rc;
      ndx++;
      if (ndx >= numChars) {
        ndx = numChars - 1;
      }
    }
    else {
      receivedChars[ndx] = '\0'; // terminate the string
      ndx = 0;
      newData = true;
    }
  }
}

void updatePeltier() {
  if (newData == true) {
    uint16_t intensity = uint16_t(receivedChars[0]-48); //Temps où le Peltier est allumé en millisecondes
    if ((intensity < 1) || (intensity > 8)) intensity = 0; //protection de calculs bizarres
    analogWrite(peltierpin, 4095 * intensity);
    delay(2000); //Le pulse dure 2 secondes
    analogWrite(peltierpin, 0);    
    newData = false;
  }
}

// callback invoked when central connects
void connect_callback(uint16_t conn_handle)
{
  // Get the reference to current connection
  BLEConnection* connection = Bluefruit.Connection(conn_handle);

  char central_name[32] = { 0 };
  connection->getPeerName(central_name, sizeof(central_name));

  Serial.print("Connected to ");
  Serial.println(central_name);
}

/**
 * Callback invoked when a connection is dropped
 * @param conn_handle connection where this event happens
 * @param reason is a BLE_HCI_STATUS_CODE which can be found in ble_hci.h
 */
void disconnect_callback(uint16_t conn_handle, uint8_t reason)
{
  (void) conn_handle;
  (void) reason;

  Serial.println();
  Serial.print("Disconnected, reason = 0x"); Serial.println(reason, HEX);
}

Le programme qui roule sur l’ordi en python est le suivant :

from adafruit_ble import BLERadio
from adafruit_ble.advertising.standard import ProvideServicesAdvertisement
from adafruit_ble.services.nordic import UARTService
import array
import numpy as np
import matplotlib.pyplot as plt
import time

ble = BLERadio()

uart_connection = None

plotbuffer = []

#plt.ion()
countdatalen = 0

while True:
    if not uart_connection:
        print("Trying to connect...")
        for adv in ble.start_scan(ProvideServicesAdvertisement):
            if UARTService in adv.services:
                uart_connection = ble.connect(adv)
                print("Connected")
                break
        ble.stop_scan()

    if uart_connection and uart_connection.connected:
        uart_service = uart_connection[UARTService]
        starttime = time.time()
        while uart_connection.connected:
            #Pour envoyer des données vers l'appareil
            #s = input("Delay in s : ")
            #uart_service.write(s.encode("utf-8"))
            #uart_service.write(b'\n')
            #Pour recevoir des données
            receiveddata = uart_service.read()
            countdatalen = countdatalen + len(receiveddata)
            print(countdatalen)
            if countdatalen >= 10000:
                print(time.time()-starttime)
                break
            #print(receiveddata)
            #if receiveddata is not None:
                #print(len(receiveddata))
                #plotbuffer.append(array.array('H',receiveddata)) #convertit le bytearray en array de 16bits unsigned
                #plt.plot(array.array('H',receiveddata))
                #plt.show()

Pour tester le feedback de respiration, j’utilise le code arduino suivant :

int mot8 = 12;
int mot7 = 13;
int mot6 = 6;
int mot5 = 5;
int mot4 = 9;
int mot3 = 10;
int mot2 = 11;
int mot1 = 22;

int motarray[8] = {mot1,mot2,mot3,mot4,mot6,mot5,mot7,mot8};

int intensity = 150;

void setup() {
  delay(3000);
}

void loop() {
  //rotations
  for (byte i = 0; i < 8; i = i + 1) {
    //anti-horaire
    //analogWrite(motarray[7 - i],intensity);
    //delay(200);
    //analogWrite(motarray[7 - i],0);
    
    //horaire
    //analogWrite(motarray[i],intensity);
    //delay(200);
    //analogWrite(motarray[i],0);
  }
  
  //random (gouttes de pluie)
  /*
  delay(random(1000));
  int randompin = random(8);
  analogWrite(motarray[randompin],intensity);
  delay(100);
  analogWrite(motarray[randompin],0);
  */
  //vagues (pourrait être cool si rythmé sur la respiration)
  
  analogWrite(mot1, intensity);
  analogWrite(mot8, intensity);
  delay(800);
  analogWrite(mot1, 0);
  analogWrite(mot8, 0);
  analogWrite(mot2, intensity);
  analogWrite(mot7, intensity);
  delay(800);
  analogWrite(mot2, 0);
  analogWrite(mot7, 0);
  analogWrite(mot3, intensity);
  analogWrite(mot5, intensity);
  delay(800);
  analogWrite(mot3, 0);
  analogWrite(mot5, 0);
  analogWrite(mot4, intensity);
  analogWrite(mot6, intensity);
  delay(800);
  analogWrite(mot4, 0);
  analogWrite(mot6, 0);
  analogWrite(mot3, intensity);
  analogWrite(mot5, intensity);
  delay(800);
  analogWrite(mot3, 0);
  analogWrite(mot5, 0);
  analogWrite(mot2, intensity);
  analogWrite(mot7, intensity);
  delay(800);
  analogWrite(mot2, 0);
  analogWrite(mot7, 0);
 
  //pulsation (même chose, synchronisé sur la respiration ça serait cool)
  //(Ca ressemble un peu aux papillons dans le ventre comme effet
  /*
  for (byte value = 50; value < intensity; value++){
    for (byte i = 0; i < 8; i = i + 1) {
      analogWrite(motarray[i],value);
    }
    delay(50);
  }
  */
}

Discussion

Je commence de plus en plus à avoir la question qui trotte en arrière pensée lorsque je travaille sur mes créations : est-ce que ce projet pourraît être un produit? Dans le cas présent, la réponse est non, pour plusieurs raisons. Il y a trop de broches à foin et de colle chaude pour que ça ne demande pas un redesign assez substantiel.

Le capteur de respiration basé sur le caoutchouc conducteur est peu fiable, peu robuste, peu précis, comporte une bonne part d’hystérésis, est difficile à calibrer. Ça marche quand on prend le temps de le faire marcher. Il faut que la ceinture soit fermée avec la bonne tension, pour que l’extension du fil soit maximale et directement relié à la respiration. Cela implique donc que la ceinture soit placée à la bonne place sur les abdominaux à la hauteur du diaphragme, avec une pression assez serée, qui peut rapidement être inconfortable. Le caoutchouc ne peut pas être soudé, il doit être pris en serre contre du métal. Dans philati, j’utilisais des pinces crocodiles. Ici j’utilise un simple noeud autour de la broche métallique. Ça peut tomber facilement et ce n’est pas robuste. Pour une version plus fiable, il faudrait utiliser un crimp avec une ferrule. La meilleure option serait de le coudre directement sur le tissu élastique, afin de rendre le positionnement plus répétable.

Ensuite, la résistance dépend de la longueur, j’ai donc prévu un trimpot afin d’ajuster la plage du pont de Wheatstone à la résistance médiance. Cet ajustement est assez artisanal et doit être fait en portant la ceinture et en regardant la pleine amplitude de la respiration. J’utilise un amplificateur d’instrumentation pour limiter le bruit. Le circuit doit être alimenté à batterie pour éviter de capter le bruit provenant de l’ordinateur par un câble USB.

Le gain est fixé par une résistance, et les fréquences de coupure des filtres analogiques sont aussi fixées par les composantes physiques. C’est donc peu flexible et peu performant, mais c’est facile à faire. Le signal provenant du fil de caoutchouc est assez faible, on parle d’une variation de résistance d’environ 100 Ohm.

En conclusion, le capteur de respiration est difficile à utiliser, doit être potentiellement réajusté à chaque fois qu’on le porte, peu confortable et peu précis.

Pour ce qui est de la partie haptique du projet, plusieurs problèmes ont également été soulevés. Le moteur vient déjà avec un fil, mais est néamoins difficile à souder et peu solide car très petit. J’ai dû souder des rallonges avec des câbles socket female 2,54mm pour brancher dans mon connecteur soudé sur mon PCB. L’assemblage a été assez fastidieux. L’ordre des moteurs a aussi été changé, mais ça s’ajuste facilement dans le firmware.

Le problème principal des moteurs en rotation est le flou artistique dans la vibration produite. Leur accélération est pas toujours pareille, la vibration se couple à l’anneau au complet, même s’il est en TPU et même si le moteur est collé sur une mince bande. Il est difficile de discerner la source exacte, d’autant plus que le couplage mécanique avec la peau et les muscles est plutôt lousse. Pour un meilleur effet, je crois qu’il faudrait carrément coller le moteur à la peau (avec du tape genre) mais ça devient beaucoup trop invasif. De plus, la vibration devient vite désagréable, un peu comme un chatouillement raté, c’est plus gossant qu’autre chose. Le fréquence de la rotation n’est pas la bonne, c’est trop rapide pour être précisément détecté, et trop lent pour être confortable. Le muscle et le cerveau ne savent pas trop comment réagir à ce stimuli.

Ce qui est intéressant comme essai, c’est de pouvoir donner une phase au moteur, et ainsi créer un mouvement. Ici, j’ai essayé de faire un mouvement de haut en bas sur le ventre, partir du diaphragme et descendre les abdominaux, puis remonter, dans le but de donner un cue sur la respiration. C’est possible d’utiliser cela pour synchroniser sa respiration sur ce rythme, mais ça demande tout de même une bonne concentration. Puisque la vibration ne correspond pas du tout au serrement/desserrement des abdominaux, elle crée une sorte de bruit biomécanique, qui désoriente un peu ses perceptions. C’est trop grossier, pas assez confortable. Tout bouge trop. Je ne sais pas non plus quel serait l’effet d’une couche de graisse, mais d’après moi ça ne serait probablement pas glorieux. Finalement, c’est un endroit assez intime le ventre, je ne suis vraiment pas certain que les gens acceptent de porter une ceinture à cet endroit. On n’est pas si loin du bas du ventre, et mon projet n’a pas de prétention érotique.

Conclusion

L’idée derrière ce projet, qui est de mesurer la respiration et d’offrir un feedback haptique pour la synchroniser sur un rythme quelconque, ou entre différents porteurs de l’appareil, est toujours intéressante et mérite d’être explorée davantage. Je vais devoir toutefois repasser sur la planche à dessin et repenser à peu près tout de zéro. Rien dans cette version ne rencontre les critères minimaux pour être intégré dans un prototype viable. On lâche pas! 🙂