laser

Mesure du phénomène de « frequency pulling » dans un laser He-Ne à deux modes axiaux par détection hétérodyne

Frederik laser, optoélectronique, radio

Cela fait longtemps que je veux faire de la détection hétérodyne, et j’ai récemment eu l’occasion de m’y mettre avec mon laser He-Ne qui a la particularité d’avoir deux modes axiaux séparés par 1GHz.

Matériel

L’idée, c’est d’utiliser une photodiode assez rapide (temps de montée <1ns) branchée sur un récepteur radio dont la plage de fréquence est suffisamment élevée pour capter le signal. J’ai donc choisi d’utiliser ma radio logicielle rtl-sdr de Noo-Elec qui peut se synthoniser jusqu’à 1,7GHz avec une largeur d’acquisition de 2,4MHz. La photodiode est la FDS02 de thorlabs et un temps de montée de 47 ps et de descente de 246 ps. L’impédance de ma radio est de 50Ohm et la capacitance de jonction de la photodiode non-biaisée est de 2pF, ce qui fait théoriquement que le circuit peut observer des signaux jusqu’à 60GHz avant de perdre 3dB. Je voulais mettre toutes les chances de mon côté, étant donné que le bruit de mon récepteur radio est tout de même élevé. La photodiode coûte 90$US et la radio logicielle, 35$US, le laser He-Ne reste le plus cher dans tout ça, à 260$US sur ebay. On peut accomplir de la science vraiment intéressante à faible budget!

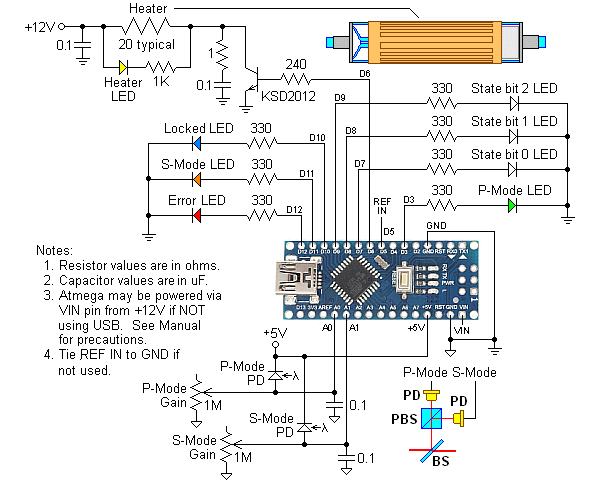
La construction est simple : j’ai soudé les deux broches de la photodiode sur un câble SMA coaxial relié à la radio. La photodiode est placée directement dans le faisceau de sortie du laser. La radio est branchée dans un port USB de l’ordinateur et le programme Gqrx est utilisé pour synthoniser la fréquence hétérodyne et afficher la FFT en temps réel.

Mesure

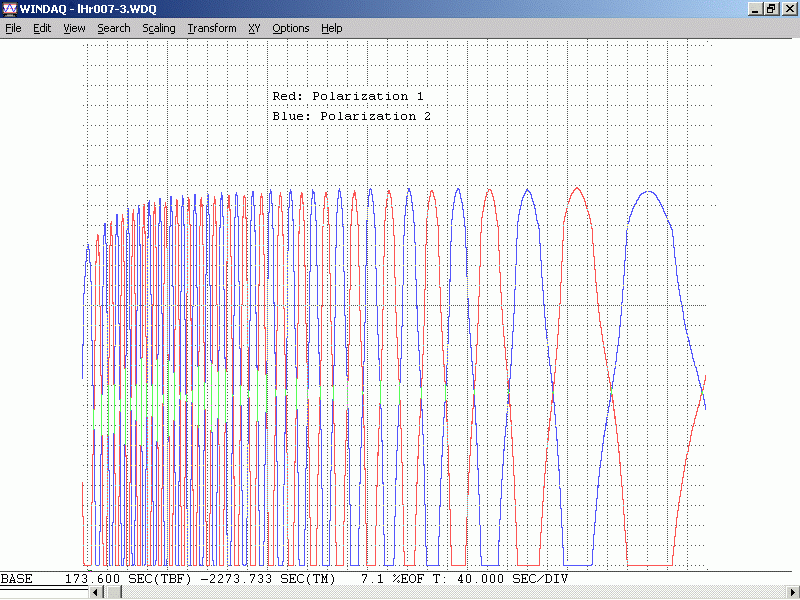
Voici une capture d’écran vidéo du signal obtenu sur ma radio :

Discussion

La cavité du laser fait 14cm. Cela veut dire que les modes axiaux supportés sont espacés de v = c/2d = 3e8/(2*0,14) = 1,071GHz. Ce calcul rapide m’a permis de rapidement scanner la radio pour trouver la fréquence du phénomène, autour de 1,08GHz. Le signal à 1,08GHz pile est évidemment un contaminant radio provenant de l’environnement, probablement de l’aéroport de Québec dans ce cas-ci puisque c’est dans la bande réservée à l’aviation.

Le fasiceau du laser He-Ne est à 632nm, ce qui fait que la fréquence optique est de 4,7*10^14Hz, ce qui est beaucoup trop rapide pour être capté par n’importe quelle électronique. Avec la détection hétérodyne, ce qu’on mesure, c’est l’enveloppe du battement, qui a une fréquence de | f1 – f2 |, soit la différence entre les fréquences des deux modes. Cela est rendu possible parce que les deux modes tombent exactement au même endroit sur la photodiode, qui répond à l’intensité lumineuse du signal total.

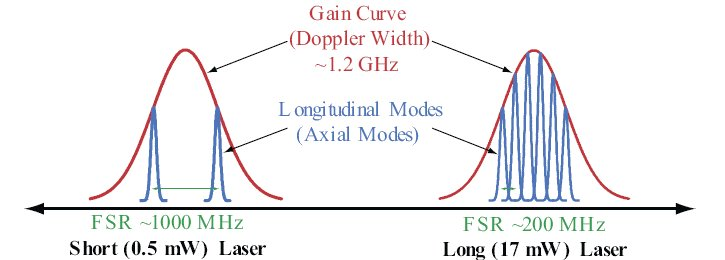
Au départ, je m’attendais à mesurer un signal plutôt stable, qui s’allume et s’éteint selon le nombre de modes dans la cavité. En effet, puisque le laser se réchauffe au départ, le verre du tube se dilate petit à petit, ce qui joue sur la longueur de la cavité, et donc sur la fréquence des modes supportés. La courbe de gain reste peu impactée par ce phénomène (je crois), cela signifie que les modes se promènent à l’intérieur de cette courbe, et qu’on a tantôt un, tantôt deux modes présents, avec une fréquence qui reste à ±1,5GHz (la largeur de la courbe de gain dans le laser He-Ne due au « doppler broadening »). Ou, à la rigueur, si le verre du tube se dilatait de l’ordre de 100 microns ou plus dû au réchauffement, on observerait une diminution progressive de la fréquence de battement d’environ 1MHz.

Or, un autre effet est observé, soit une variation rapide et dans les deux sens (un va-et-vient, à deux fréquences différentes) de la fréquence hétérodyne, avec un amplitude d’environ 400kHz. Ce sont les espèces de paraboles couchées que l’on observe dans la FFT au début de la vidéo. La vitesse de ce phénomène ralentit au fur et à mesure que le laser se réchauffre, jusqu’à atteindre un point de relative stabilité. Cela prend environ 30min de réchauffement pour atteindre ce moment, ce qui correspond bien avec mes autres mesures de stabilité en polarisation. À la fin du vidéo (minute 2, qui correspond dans la réalité à la minute ~30), on voit comment le laser devient stable, mais sensible à toute fluctuation de température, puisqu’il est exposé à l’air libre sans contrôle sur le transfert thermique. On atteint tout de même déjà une stabilité sur la fréquence à moins de 100kHz.

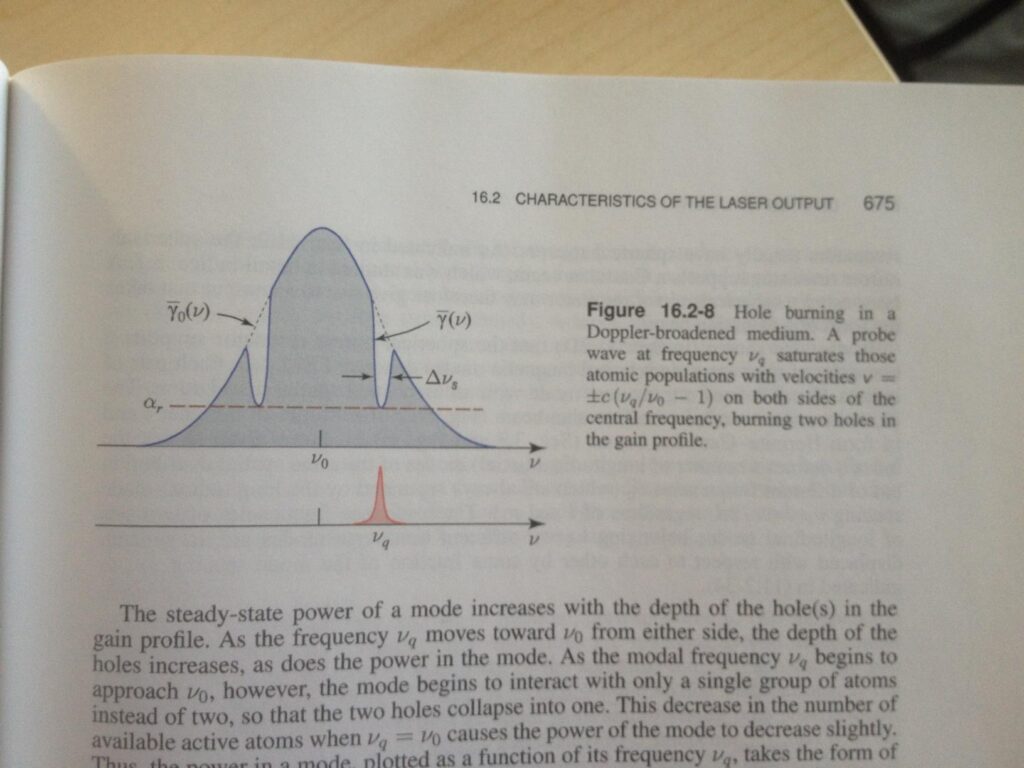
La question est donc : qu’est-ce qu’on observe? Pourquoi? Après plusieurs heures de recherches dans mes manuels, dont nottament le « Lasers » de Siegman et le Saleh et Teich, Fundamentals of photonics part II, j’ai compris que le phénomène s’appelle « frequency pulling ». Voici les deux pages traitant de ce sujet dans le Saleh et Teich :

En bref, ce que j’en comprends c’est que l’interaction des photons avec le milieu de gain crée un léger déphasage qui dépend de la position sur la courbe de gain (donc de la fréquence). Cette non-linéarité est tracée à la figure 16.1-3. Le déphasage se traduit en un changement de la fréquence du mode supporté, puisqu’un aller-retour dans la cavité doit donner exactement un multiple de 2pi en phase pour que l’onde soit stationnaire. Plus on s’éloigne du centre de la courbe de gain, plus le déphasage augemente, donc plus la fréquence des modes est « tirée » vers le centre.

Lorsque le laser se réchauffe, les deux modes se promènent le long de cette courbe de non-linéarité, ce qui fait que la différence entre leurs fréquences augmente, puis diminue. Par exemple, supposons qu’un mode est plus proche du centre et que l’autre apparaît tout juste. L’effet du frequency pulling sera maximal, donc la fréquence hétérodyne sera la plus basse. Ensuite, lorsque les deux modes sont à égale distance par rapport au centre de la courbe de gain, la fréquence hétérodyne atteint un maximum, puis redescend à sa valeur initiale de manière symétrique. Cela explique bien la forme de parabole observée dans la FFT du signal.

La seule chose que je ne m’explique pas, c’est le saut périodique d’environ 500kHz lorsque les modes apparaissent et disparaissent. (Le phénomène de parabole est observé tantôt à 1079,5MHz, tantôt à 1080MHz. Il faut bien garder quelques mystères!

À la page 469 du Siegman, un calcul de frequency pulling est fait pour le cas d’un laser He-Ne avec 10% de gain en puissance par aller retour. Cela donne un ratio de 1,6*10^-3. Dans mon cas, j’ai seulement deux modes et j’observe un ratio de ~400kHz / 1GHz = 4*10^-4. Il y a seulement un facteur 4 de différence, ce qui s’explique sûrement par les différences entre les paramètres de mon laser et ceux de l’exemple. Cela me permet toutefois d’évaluer le gain en puissance par aller-retour à (4*10^-4)*2*pi*2 = 0,5%. C’est surprenamment peu, mais le laser est tout de même très court. Étant donné que je ne me suis pas penché sur les détails du calcul et ses approximations, je ne suis pas très confiant sur ce dernier chiffre, c’était davantage pour montrer qu’on peut se servir de la mesure pour calculer d’autres paramètres du laser.

Dans une prochaine expérience, il serait intéressant d’utiliser la détection hétérodyne avec une diode laser, pour voir quels autres phénomènes seraient observables.

Pourquoi un laser He-Ne a-t-il deux modes aux polarisations orthogonales?

Frederik laser

Il est de ces questions qui nous empêchent de dormir la nuit. Je me suis repensé sur mon projet de Fabry-Perot et de laser He-Ne stabilisé, avec l’intension de peut-être utiliser une photodiode en détection hétérodyne.

Jusqu’à présent, je pensais que le laser He-Ne avait un seul mode axial dans la cavité, mais qu’il se découlait en deux polarisations. Ainsi, les deux polarisations avaient exactement la même fréquence (avec une très petite largeur de raie). C’était naïvement en prenant comme prémice que c’est ce qu’il se passe dans une cavité, un guide d’onde, etc. Il faut tout le temps faire x2 le nombre de modes pour tenir compte des deux polarisations.

Il n’y a aucun contrôleur de polarisation dans un He-Ne cheap, ni fenêtre de Brewster, ni lame quart d’onde, etc.

Je ne sais plus exactement d’où m’est venue l’idée d’investiguer davantage le sujet. Je crois que je cherchais une façon d’avoir deux fréquences avec un He-Ne. En allant sur le site de Thorlabs, je suis tombé sur le diagramme suivant : (source : https://www.thorlabs.com/newgrouppage9.cfm?objectgroup_id=10776 )

Mon fournisseur de laser (siliconsam) a beaucoup de choses à dire sur le sujet, c’est difficile de faire le tri dans toute cette information : https://www.repairfaq.org/sam/laserhen.htm

En bref, la transition qui nous intéresse dans le Néon, qui produit la raie à 632,8nm, a une largeur d’environ 1,5GHz (le chiffre exact varie selon les sources et probablement les calculs). Cela est dû au fait que les atomes dans le gaz à température ambiante, ont une distribution gaussienne de vitesse par rapport à l’axe du laser. Par effet Dopler, cela crée une distribution similaire dans la courbe de gain selon la fréquence pour l’émission stimulée. En choisissant la longueur de la cavité, on peut ainsi construire un laser qui a exactement deux modes longitudinaux.

Avec v=nc/2L, on trouve L = nc/2v. Cela fait L = 2*3e8m/s/2*1,5e9Hz = 0,2m. Avec un laser de 20cm de long (c’est ce que j’ai), seulement deux modes de la cavité peuvent tomber dans la largeur de la courbe de gain. Ok cool. Mais maintenant, pourquoi ces deux modes ont-ils une seule polarisation, et qui plus est, toujours orthogonale à l’autre?

En fait, au gré des changements de température, la longueur de la cavité change légèrement, ce qui fait que les modes se « promènent » dans la courbe de gain. Si rien n’est stabilisé, la polarisation se promène cycliquement entre les deux extrêmes, puisque les modes ont des positions (et donc des intensités) variables dans la courbe de gain. Cette propriété est utilisée dans la méthode de stabilisation de mon laser. Puisque les deux modes se séparent parfaitement par leur polarisation, on peut s’arranger pour contrôler la longueur de la cavité au moyen de la température du tube, afin que les deux modes gardent leur position à l’intérieur de la courbe de gain, et donc leur fréquence.

En lisant davantage, je suis tombé sur le concept de « spectral hole burning in a Doppler-broadened medium » (p.674 du Saleh et Teich). En bref, à cause de la symétrie de la cavité (aller-retour du faisceau), les atomes qui ont la vitesse +v et -v sont saturés. Pourtant, cela ne peut pas être la source du phénomène, puisque les modes se promènent au-delà de cet effet miroir, et les polarisations restent définies et orthogonales.

Se pourrait-il qu’il y a ait le même genre de hole burning dans la courbe de gain, mais pour la polarisation? Difficile à trouver dans les internets. Google me ramène encore à la page de siliconsam, je trouve un extrait pertinent :

Polarization of Longitudinal Modes in HeNe Lasers

It is well known that adjacent longitudinal modes in red (632.8 nm) HeNe lasers (at least) tend to be orthogonally polarized as discussed above. This is a weak coupling as a magnetic field, Brewster plate, or even some asymmetry in the cavity can affect it or kill it entirely. And some lasers will cause the polarization to suddenly flip as modes cycle through the gain curve. However, the majority of modern well designed red HeNe lasers will exhibit this phenomenon.

This is not necessarily true of « other color » HeNes. My informal tests suggest that in general it is *not*. Long green (543.5 nm), short and long yellow (594.1 nm), and medium length orange (611.9 nm) random polarized HeNe laser heads all exhibited varying degrees of erratic behavior with respect to polarization. Usually, modes when part of the way through the gain curve and then either flipped abruptly or oscillated between polarizations for a short time and then flipped. The long yellow head liked to have pairs of adjacent modes with the same polarization but exhibited the flipper behavior as well. However, adding a modest strength magnet near the long green seemed to force it to behave with adjacent modes having orthogonal polarization. I have no idea if this is significant or the long green HeNe was simply a cooperating sample.

But what is the underlying cause?

(From: A. E. Siegman (siegman@stanford.edu).)

The reason that HeNe lasers can run – more accurately, like to run – in multiple axial modes is associated with inhomogeneous line broadening (See section 3.7, pp. 157-175 of my book) and « hole burning » effects (Section 12.2, pp. 462-465 and in more detail in Chapter 30) in the Doppler-broadened laser transitions commonly found in gas lasers (though not so strongly in CO2) and not in solid-state lasers.

The tendency for alternate modes to run in crossed polarizations is a bit more complex and has to do with the fact that most simple gas laser transitions actually have multiple upper and lower levels which are slightly split by small Zeeman splitting effects. Each transition is thus a superposition of several slightly shifted transitions between upper and lower Zeeman levels, with these individual transitions having different polarization selection rules (Section 3.3, pp. 135-142, including a very simple example in Fig. 3.7). All the modes basically share or compete for gain from all the transitions.

The analytical description of laser action then becomes a bit complex – each axial mode is trying to extract the most gain from all the subtransitions, while doing its best to suppress all the other modes – but the bottom line is that each mode usually comes out best, or suffers the least competition with adjacent modes, if adjacent modes are orthogonally polarized.

There were a lot of complex papers on these phenomena in the early days of gas lasers; the laser systems studied were commonly referred to as « Zeeman lasers ». I have a note that says a paper by D. Lenstra in Phys. Reports, 1980, pp. 289-373 provides a lengthy and detailed report on Zeeman lasers. I didn’t attempt to cover this in my book because it gets too complex and lengthy and a bit too esoteric for available space and reader interest. The early (and good) book by Sargent, Scully and Lamb has a chapter on the subject. You’re probably aware that Hewlett Packard developed an in-house HeNe laser short enough that it oscillated in just two such orthogonally polarized modes, and used (probably still uses) the two frequencies as the base frequencies for their precision metrology interferometer system for machine tools, aligning airliner and ship frames, and stuff like that.

C’est quand même nice qu’il ait écrit directement à Siegman (Le livre est bien sûr Lasers, et je l’ai dans ma bibliothèque! Merci le cours de laser de l’université!)

Il se passe donc un effet particulier avec cette transition précise, dans les orbitales de l’atome de Néon. L’effet Zeeman, même sans champ manétique externe est présent et influence la polarisation. Ainsi, les deux modes compétionnent quand même pour les mêmes atomes, et la manière de les rendre le moins couplés possible est d’avoir des polarisations complètement orthogonales, de manière à optimiser le gain sur les deux modes en même temps.

De nombreux doctorats se sont écrits sur le sujet, et j’ai pas la prétention d’avoir tout compris, mais après ces recherches de plusieurs heures, je crois avoir trouvé une certaine paix d’esprit face à ce questionnement.

Stabilisation des modes d’un laser He-Ne

Frederik laser, polarimètre

En 2016, pour compléter mon projet d’interféromètre de Michelson, j’avais acheté un laser HeNe en kit, sur ebay. Le tube était tout nu, le power supply était fourni, et le tout venait avec des pièces d’électronique pour stabiliser les modes de polarisation du laser. Puisque la polarisation avait peu d’impact dans mon interféromètre, j’ai simplement utilisé le tube tel quel, en obtenant des bons résulats (ma vidéo ici : https://youtu.be/Cea9mbSiblM )

Récemment, dans mon expérience avec mon polarimètre, j’ai observé une oscillation entre deux polarisations linéaires orthogonales. Le tout se comporte comme si le système est une somme de deux ondes avec une polarisation en x et y (selon une orientation spatiale arbitraire autour de l’axe du faisceau) qui oscillent. En lisant un peu, justement sur le site du kit de stabilisation, j’ai compris que lorsque le laser se réchauffe, le gain est plus élevé pour une polarisation qu’une autre, ce qui fait qu’elle domine momentanément l’émission. Puisque le tube contenant le gaz est à l’intérieur d’un autre tube, ce réchauffement prend une éternité et est soumis aux variations des conditions environnementales (convection, etc.). L’idée de sliconsam (pseudo sur ebay) alias repairfaq.org, est de chauffer le tube en se régulant sur les valeurs des deux polarisations. Pour cela, il utilise un polarizing beam splitter cube orienté de manière à respecter l’orientation naturelle des deux modes du laser. Les instructions se trouvent ici : http://repairfaq.org/sam/manuals/stabins5.htm

Le schéma électronique est le suivant :

Source : http://www.repairfaq.org/sam/uSLC1/uSLC1.htm

Une fois assemblé, ça ressemble à ceci :

J’ai rajouté un ampli transimpédance pour diminuer le bruit. Mon montage optique ressemble à un gros blob de colle, et fixé avec un tie-wrap sur le miroir du faisceau secondaire (ne le dites pas à personne, c’est un peu gênant).

Optique et électronique pour la stabilisation du laser. En vert, le miroir du laser, le cube dépasse un peu du motton de colle chaude. Les deux photodiodes sont à même la surface. Le tout tient à un angle d’environ 15degrés par rapport à l’horizontale, défini par la partie du laser qui a l’entrée de remplissage du gaz.

La pièce imprimée en 3D est celle-ci, mais elle marchait moyen, c’était juste pour me donner une base :

$fn=50;
//rotate([0,90,0]){
difference(){
cube([13,15,15],center=true);
#translate([-6.5,-7.5,0]) cube([13,15,10]);
translate([7,0,0]) rotate([0,-90,0]) cylinder(d=6.5,h=5); //miroir du laser
cube([4.5,4.5,4.5],center=true); //polarizing beam splitter
translate([0,-4.5,0]) cube([7,6,4.5],center=true); //photodiode
translate([-4.5,0,0]) cube([5,7,4.5],center=true);
}

Dans la version actuelle de ce kit, siliconsam fournit un pcb qui contient déjà cet assemblage un peu délicat. Mais toujours pas de manière de le fixer au tube. Bref mon montage n’est pas idéal, mais il fonctionne bien. Le résultat final ressemble à ceci (en incluant ma monture pour ajuster les angles et la hauteur déjà assemblée de mon projet d’interféromètre) :

En utilisant le firmware déjà présent sur l’arduino, qui contient entre autres un PWM (je n’ai pas lu tous les détails), j’ai réussi à observer l’évolution du réchauffement. On voit clairement une accélération de l’oscillation lorsque l’on part le heater, puis un ralentissement lorsque l’algo de stabilisation commence à embarquer.

Source : http://repairfaq.org/sam/manuals/stabins5.htm

Contrairement aux promesses, je n’ai pas réussi à obtenir un lock parfait, cela durait quelques minutes, puis le laser sortait de sa zone de stabilité et recommençait à osciller. Peut-être qu’il y a un bug, je vais essayer d’updater le firmware. Il y a aussi le fait que je l’ai utilisé en hiver avec une température externe démesurément basse de notre mois de janvier, dans une pièce propice aux courants d’air. En outre, le tube n’est pas isolé plus qu’il faut. Prochaine étape, faire un boitier pour tout ça qui isole mieux des conditions environnementales tout en permettant la flexibilité du montage. Peut-être que ça aiderait aussi le délai avant l’obtention d’un lock, qui était d’environ 45min-1h. Disons qu’il ne faut pas être pressé avant de faire des mesures! En tout cas, c’est très intéressant d’avoir un laser contrôlé en polarisation, pouvant fournir l’une ou l’autre sur demande, avec une stabilité en intensité qui dure plusieurs minutes.